Anyone who has taken a course in Group Theory has encountered this type of exercise: listing all groups of a given order (up to isomorphisms).

In this article, I want to summarize some of the most commonly used techniques for answering this question, applying them to the case of groups of order 18.

Sylow’s theorem

The first thing to do is determine the possible numbers of subgroups with cardinality equal to some maximal power of a prime, using the well-known Sylow theorems. These subgroups, called Sylow p-subgroups, will help simplify the problem. In fact, the group we want to study can be expressed as a direct or semidirect product of its Sylow p-subgroups, so we only need to examine all possible combinations of such products (divide et impera!)

As \(18 = 2 \cdot 3^2\), there could be one or more Sylow 3-subgroups (of order 9), and one or more Sylow 2-subgroups (of order 2).

Sylow’s theorems tell us that there is only one Sylow 3-subgroup, let’s call it \(H_3\), while there could be either 1, 3, or 9 Sylow 2-subgroups. The 3-Sylow is abelian because it is a group of cardinality a squared prime. Moreover, the 3-Sylow is also a normal subgroup (when there is only one p-Sylow for some prime p, this unique p-Sylow is a normal subgroup).

Case 1: there is one 2-Sylow

If there is just one 2-Sylow, then is it normal. Since the 3-Sylow and 2-Sylow are both normal subgroups, their product is isomorphic to their direct product:

The easiest case to discuss is that with only one 2-Sylow. Let’s call it H2. Then, we have two normal subgroups, therefore, their subgroup product is isomorphic to their direct product, which is isomorphic to G.

Then, \(G\) is abelian, and, by the theorem of classification of finite abelian groups, we have

Case 2: there are more than one 2-Sylow

Let’s now consider the case where there is more than one 2-Sylow subgroup (3 or 9).
Let’s call H2 one of the Sylow 2-subgroups. Since H2 is not a normal subgroup, the subgroup product of H2 and G3​ is isomorphic to a semidirect product.

Recall that products between elements in a semidirect product of groups are defined by a homomorphism that assigns to each element of the non-normal subgroup an automorphism of the normal subgroup. Thus, the way \(H_2\)​ and \(H_3\)​ combine depends on this homomorphism, and for each homomorphism, we will have a different structure for the group \(G\).

Let’s call \(\Phi\) our automorphism. Since \(H_2\) has only two elements – call them \(h\) and \(1\) – we only need to select \(\Phi(h)\) because \(\Phi(1)\) must be the identity. Moreover, we must have \(\Phi(h) \circ \Phi(h) = \Phi(1) = id\).

At this point, all that remains to do is to find the automorphisms of $H_3$$H_3$​ that, when composed with themselves, yield the identity. Each of these automorphisms will allow us to define a $\Phi$$\mathrm{\Phi }$, and thus a semidirect product.

The 3-Sylow is \(C_9\)

However, we need to distinguish between two cases because, as we saw earlier, the 3-subgroup can be a cyclic subgroup of order 9 or the direct product of two subgroups of order 3. Let’s consider the first case. To clarify the next steps, let’s write as follows the elements of the 3-subgroup:

Since it is a cyclic group, any automorphism is determined by the image of a generator.

This leads us to two automorphisms: the identity and the automorphism that sends every other element in its opposite.

We use the “opposite” automorphism as \(\Phi(h)\).

Therefore, let’s recall the definition of semidirect product and apply it to our groups with the $\Phi$$\mathrm{\Phi }$ we’ve just obtained:

Now, let’s find a presentation of the group G obtained in this way. We use the generators

where the first element of each couple is in \(H_3\) and the second in \(H_2\), then we have the relations

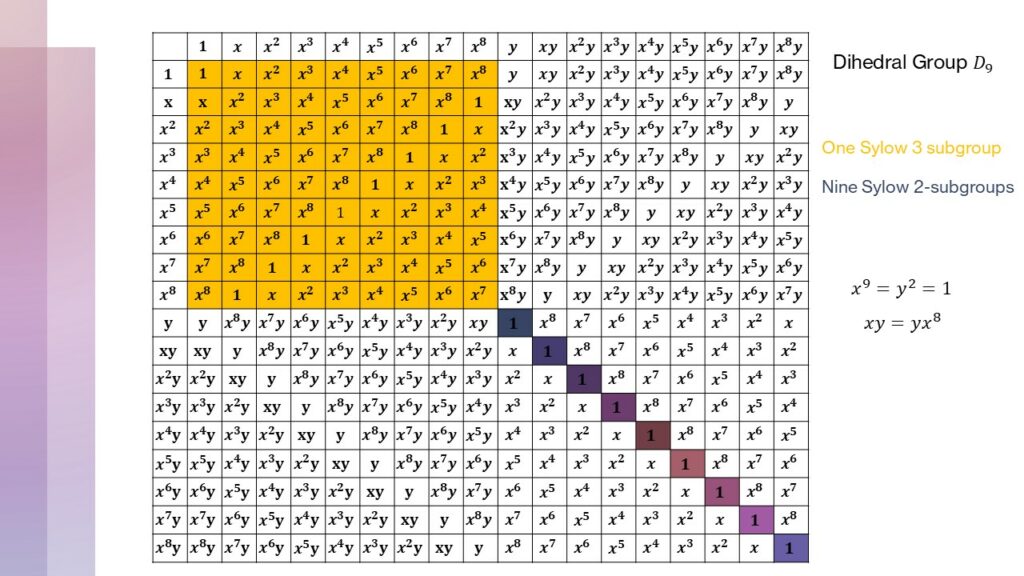
We immediately recognize that the group we’ve just found is \(D_9\), the group of symmetries of the regular nine-sided polygon.

The 3-Sylow is \(C_3\times C_3\)

With similar calculations, we find that all homomorphisms produce two groups: the first is given by the automorphism of \(C_3\times C_3\) that maps each generator to its inverse, and the other is given by the automorphism that swaps the generators. Here are the presentations of the two resulting groups: