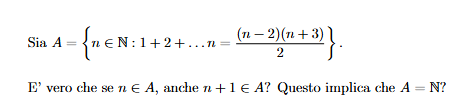
Il principio di induzione si usa per dimostrare che una certa proprietà è vera per tutti i numeri naturali o per tutti i numeri naturali maggiori di un certo numero.
Una dimostrazione per induzione consiste di due passaggi: il passo base e il passo induttivo.
Nel passo base si deve dimostrare che la proprietà è vera per un certo numero o per un insieme di numeri (che saranno il più piccolo o i più piccoli numeri per i quali vale la proprietà).
Nel passo induttivo, si deve dimostrare che se la proprietà è vera per un certo n, allora è vera per il successivo n+1.
Anche se il passo induttivo è generalmente più difficile da dimostrare del passo base, non bisogna dimenticare il passo base, senza il quale la dimostrazione non si regge.
Questo esercizio ne è un esempio. Qui si riesce a dimostrare che A è chiuso rispetto al successivo (passo induttivo), tuttavia, A è vuoto.
Assumiamo infatti che un certo n appartenga ad A e proviamo a dimostrare che n+1 appartiene ad A.
Dobbiamo quindi provare che n+1 soddisfa la proprietà che caratterizza gli elementi di A. Scriviamo quindi la somma dei numeri fino a n+1 e sfruttiamo il fatto che n appartiene ad A:
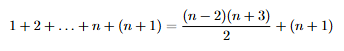
Facendo qualche calcolo, si vede che l’espressione sulla destra si può ricondurre alla proprietà caratteristica di A:
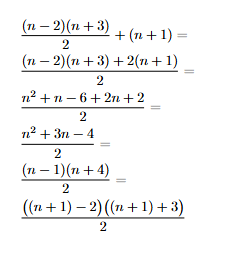
Dunque, n+1 appartiene ad A.
Domandiamoci ora se esistono numeri naturali che appartengono ad A.
In verità, sappiamo che esiste una formula per la somma dei primi n numeri naturali:
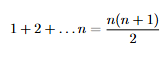
Per trovare quali numeri appartengono ad A, possiamo eguagliare l’espressione sulla destra a (n-2)(n+3)/2 :
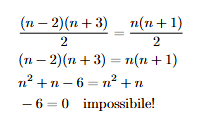

Lascia un commento